2024年遼寧大學非全日制研究生招生考試《數學分析》考試大綱
1.實數集與函數
1.1 掌握實數概念及其基本性質。掌握實數絕對值的概念和有關的不等式。
1.2 掌握鄰域概念, 掌握確界定理。
1.3 掌握函數的概念及各種表示方法,掌握復合函數和反函數的概念。
1.4 掌握有界函數與無界函數、單調函數、奇函數和偶函數、周期函數等概念。
1.5 掌握六類基本初等函數的定義和性質。
1.6 掌握常用的幾個非初等函數，如符號函數，狄利克雷函數等。
2. 數列極限
2.1 掌握數列極限的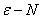
的定義, 會使用“
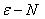語言”證明數列的極限。
2.2 正確理解和掌握收斂數列的性質。
2.3 掌握單調有界原理,致密性定理及Cauchy收斂準則。
3. 函數極限
3.1 掌握函數極限的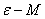
和
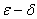定義。
3.2 掌握函數極限的性質。
3.3 掌握函數極限存在的條件, 掌握歸結原則及柯西準則。
3.4 掌握重要極限
和
及其應用。
3.5 正確理解和掌握無窮大和無窮小的概念及無窮小的階。
4. 函數的連續性
4.1 掌握連續函數的概念, 掌握間斷點及其分類。
4.2 掌握連續函數的局部性質,掌握閉區間上連續函數的性質。
4.3 掌握反函數的連續性,掌握函數的一致連續性。
4.4 掌握初等函數在其定義域上的連續性。
5. 導數與微分
5.1 掌握導數的概念及其幾何意義。
5.2 掌握求導法則,掌握參變量函數的導數法則, 掌握高階導數的求法。
5.3 掌握微分的概念及其幾何意義。
5.4 掌握微分的運算法則,了解高階微分,了解微分在近似計算中的應用。
6. 微分中值定理及其應用
6.1 熟練掌握中值定理的條件、結論和證明方法。
6.2 掌握不定式極限的求法,熟練掌握洛必達法則及其應用。
6.3 掌握泰勒公式，掌握用多項式逼近函數的思想。
6.4 會分析函數的性態,會求函數的單調區間和極值，會判斷函數的凸性和拐點,會較完善地作出函數的圖形。
由于篇幅有限，無法為同學全面展示，想要了解更多，請點擊下面附件進行下載。
您填的信息已提交,老師會在24小時之內與您聯系
如果還有其他疑問請撥打以下電話
熱門簡章
更多
東北大學
沈陽農業大學
沈陽師范大學
沈陽航空航天大學
沈陽建筑大學
微信小程序
微信公眾號
在職研APP
